15 Permutation Tests

15.1 Group Comparisons

Consider comparing two indpendent groups. Example: comparing different bug sprays

• Consider the null hypothesis that the distribution of the observations from each group is the same
• Then, the group labels are irrelevant
• Consider a data frame with counts in one column and spray label in another
• Permute the spray (group) labels
• Recalcuate the statistic
  • Mean difference in counts
  • Geomatric means
  • T-statistic
• Calculate the percentage of simulations where the simulted statistic was mroe extreme (toward the alternative) than the observed. This will create a permutation-based p-value.

15.2 Variations on Permutation Testing

Data Type, Statistic, Test Name

• Ranks, Rank Sum, Rank Sum Test
• Binary, Hypergeometric Prob, Fisher’s exact test
• Raw data, …, Ordinary Permutation Test

So-called Randomization tests are exactly oerutation tests, with different motivations.

• For matched data, one can randomize the signs
  • For ranks, the results in the signed rank test
• Permutation strategies work for regression as well
  • Permuting a regressor of interest
• Permutation tests work very well in multivariate settings

15.3 Permutation Test B v C

# Select sprays B and C
subdata <- InsectSprays[InsectSprays$spray %in% c("B", "C"), ]

# Set y as the outcome (counts in this case)
y <- subdata$count

# Set group as group labels
group <- as.character(subdata$spray)

# Test statistic here is just the difference in average between the two sprays
# Averaged out over batches
testStat <- function(w, g) mean(w[g == "B"]) - mean(w[g == "C"])

# The observed statistic here is just the test statistic applied to the outcome and group
observedStat <- testStat(y, group)

# Now we're going to resample the group labels to breka up any association between the outcome and the group labels and measure a test statistic 10,000 times 
permutations <- sapply(1 : 10000, function(i) testStat(y, sample(group)))

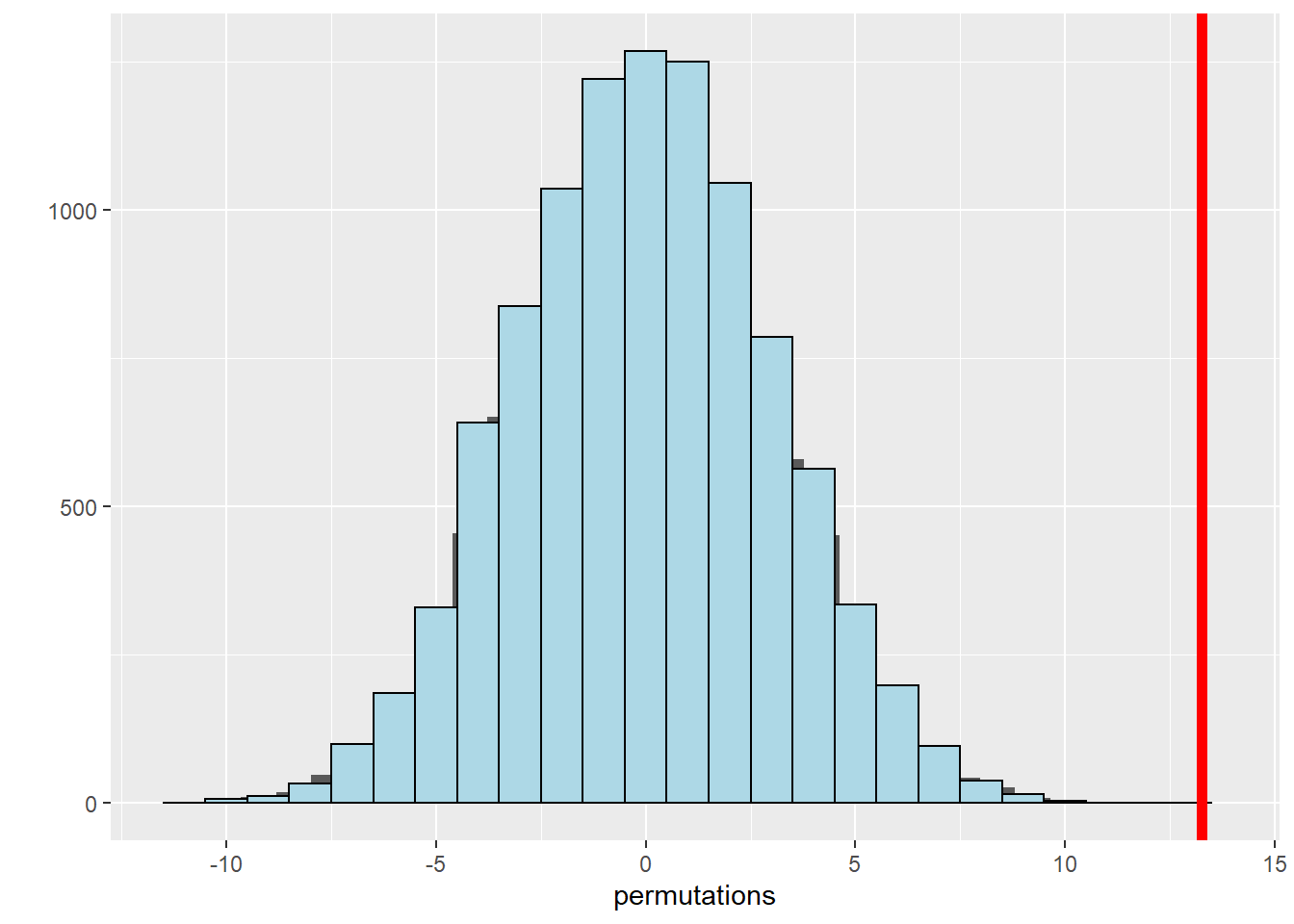
observedStat

## [1] 13.25

# Calculate the percentage of permuted test statistics that are larger or more extreme, in favor of the alternative in our observed statistic 
mean(permutations > observedStat)

## [1] 0

# Plotting a histogram allows us to see the distribution of permuted means. The red line indicates the observed mean from the original group
qplot(x = permutations) +
  geom_histogram(color = "black", fill = "lightblue", binwidth = 1) +
  geom_vline(aes(xintercept=observedStat),color="red", size=2)

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.